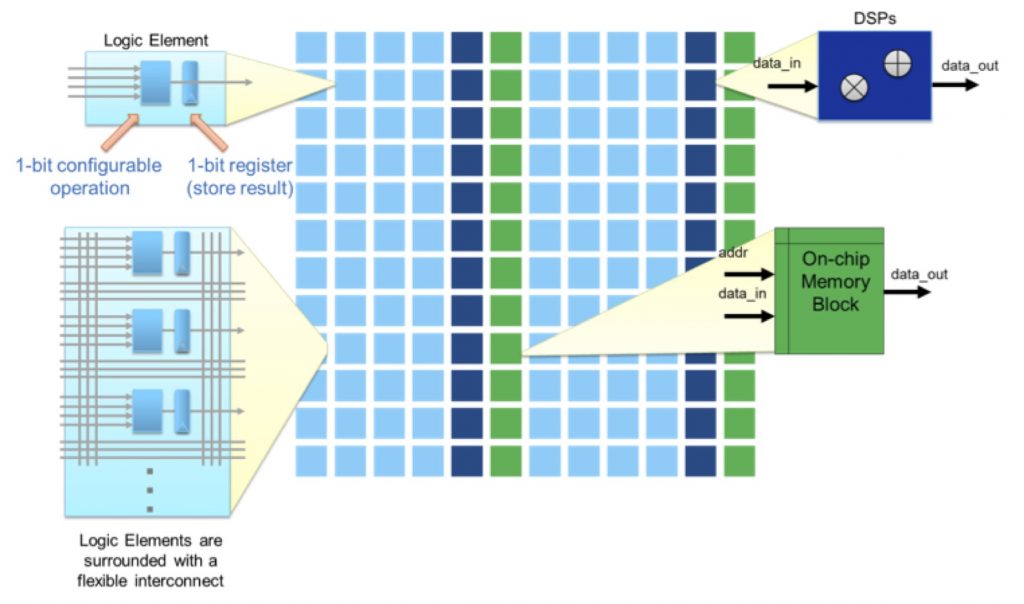
FPGAs have proven to be a compelling solution for solving deep learning problems, particularly when applied to image recognition. The advantage of using FPGAs for deep learning is primarily derived from several factors: their massively parallel architectures, efficient DSP resources, and large amounts of on-chip memory and bandwidth. An illustration of a typical FPGA architecture is shown in Figure 1.
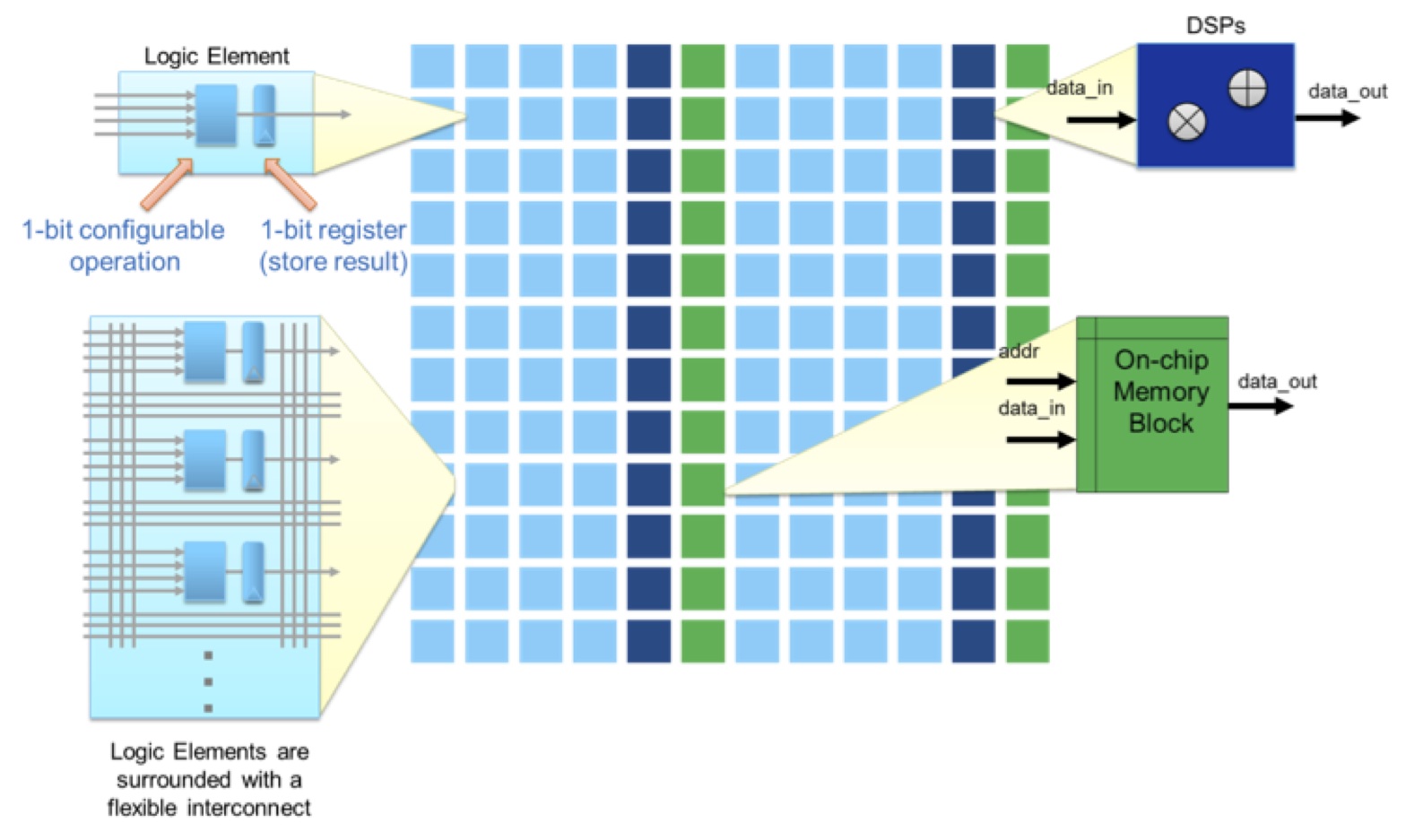
Figure 1. FPGA architecture overview
As Figure 1 illustrates, an FPGA consists of an array of configurable logic elements that compute values in parallel. These configurable logic elements can be programmed to implement any N-input function, where N is the number of inputs into the logic element, and they can also be chained together to perform more complicated tasks through their programmable interconnect as shown in the figure. Once programmed, the configured array of logic elements can be executed in parallel, leading to extremely efficient algorithm implementations.
In addition to generic-function logic elements, FPGAs include DSP blocks that provide an efficient source of numerical operations, such as the dot-product calculations that are common in deep learning algorithms. The bit-level reconfigurable nature of FPGAs means that they're not restricted to fixed word sizes during computation. FPGAs can therefore efficiently perform math operations on a wide range of numerical representations and sizes, including integer, fixed-point, and variable-precision floating point. The bit-width of the fixed-point or floating-point representation is completely up to the designer, not limited to power-of-2 type sizes.
A high-level diagram of the DSP blocks available in today’s FPGA devices is shown in Figure 2. In the diagram, data flows from left to right. The optional high-speed input (wire entering from top) and output (wire leaving out to bottom) can be used to chain multiple DSP blocks together to construct larger operations such as dot-products. Additionally, you can bypass the registers (shown as blue rectangles) in order to simplify the DSP block, as well as configure the DSP block solely as either an adder or a multiplier.
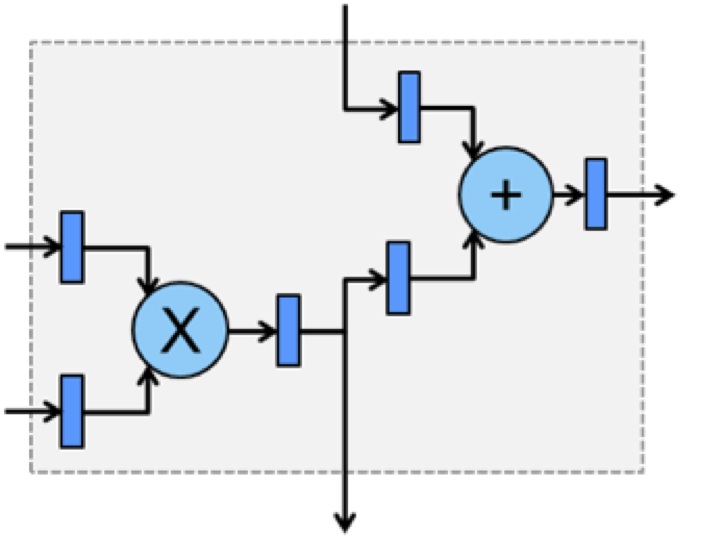
Figure 2. High-level DSP block diagram
The configurability of DSP blocks and logic elements provides an algorithm designer with the freedom to work in different numerical forms, depending on the deep learning algorithm chosen and/or varying throughput requirements. For example, if the deep learning algorithm is required to detect only a small set or class of images and accuracy is not a concern, low bit-width sized (4-bit, for example) fixed-point can be used to minimize the amount of FPGA resources used, as well as improve the overall throughput of the algorithm. Additionally, deep learning algorithms that take advantage of single bit representations of values may also benefit from being run on highly flexible FPGAs (ref: M. Kim et al, "Bitwise Neural Networks").
Lesser-known aspects of FPGAs include their large availability of both on-chip memory and bandwidth. A typical FPGA today provides on the order of 50 million bits of on-chip memory resources, and can move data across the chip at a rate of over 8 TFlops/s. This can lead to extremely efficient caching architectures, as illustrated in Figure 3.
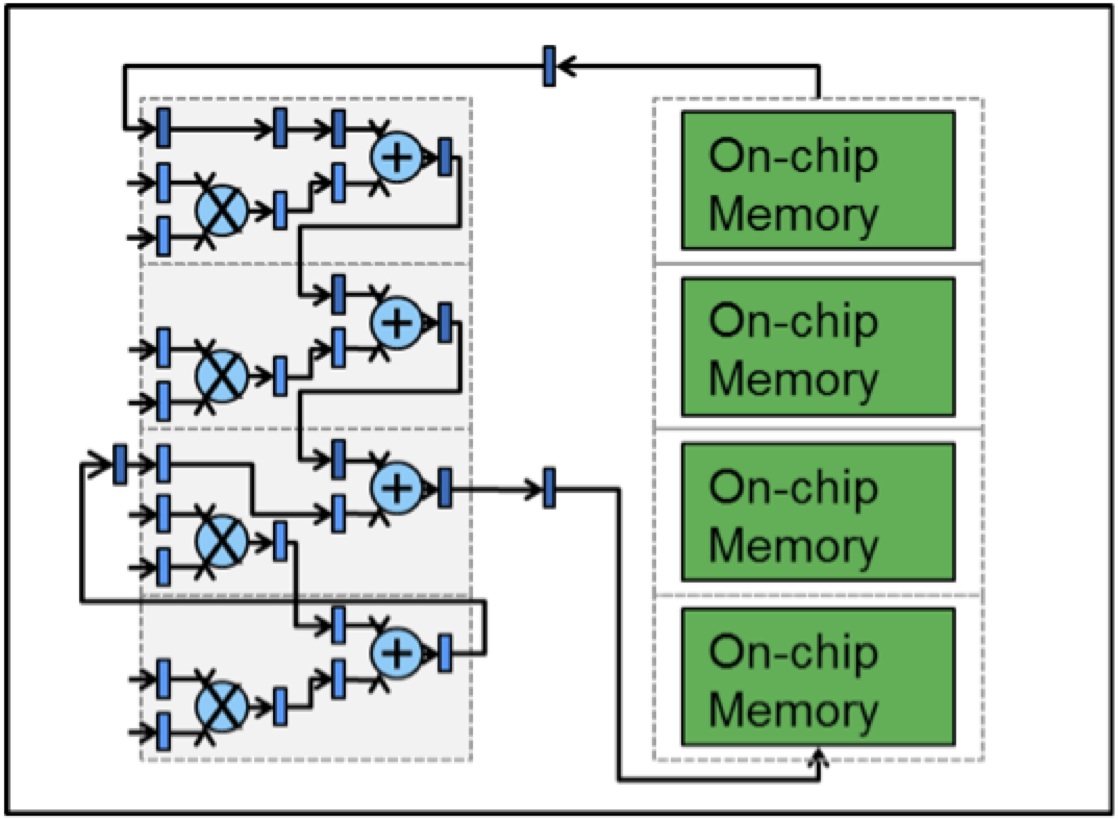
Figure 3. Dot-product circuit connected to larger internal "cache"
In Figure 3, a simple dot-product circuit is shown, which calculates the dot-product of two vectors of floating point numbers, whose partial value is stored in a FIFO-like cache. The circuit configuration performs efficient dot-product accumulations by cycling the data through the FIFO-like cache and feeding the partial results back to the dot-product circuit. This is the basic operation in the class of deep learning algorithms that consist of matrix-multiplies/convolutions.
The circuit in Figure 3 can be replicated as many times as possible on an FPGA, in order to perform many dot-product accumulations in parallel, thereby speeding up the overall deep learning algorithm. The beauty of such an approach is that as new FPGA devices grow to ever-bigger sizes, only a simple replication operation is necessary to port the exsting deep-learning algorithm to the larger FPGA device. Similarly, for use in smaller FPGAs, deep learning algorithms can be subdivided and otherwise downscaled to fit on the device at the tradeoff of reduced throughput. In the end analysis, it is the deep learning performance requirements that determine which FPGA a user should purchase and employ.
By Andrew Ling, Ph.D.
Engineering Manager, Intel Programmable Solutions Group (formerly Altera)
Utku Aydonat, Ph.D.
Staff Engineer, Intel Programmable Solutions Group
Gordon Chiu
Engineering Director, Intel Programmable Solutions Group