Quantization of Convolutional Neural Networks: Quantization Analysis

See “Quantization of Convolutional Neural Networks: Model Quantization” for the previous article in this series.

In the previous articles in this series, we discussed quantization schemes and the effect of different choices on model accuracy. The ultimate choice of quantization scheme depends on the available tools. TFlite and Pytorch are the most popular tools used for quantization of CNNs, and both support 8-bit quantization. TFlite uses symmetric per channel quantization for weights and asymmetric quantization for activations, with support for 16-bit integer activations. Pytorch quantization allows more flexibility for choosing different quantization schemes and granularity for both weights and activations.

In this article, we will review techniques for model quantization and quantization error analysis, concluding it with a list of best practices.

Network Architecture

Quantization of float-point models into 8-bit fixed-point models introduces quantization noise in the weights and activations, which leads to degradation in model performance. This performance degradation might lead to minor degradation in accuracy or a complete failure in model prediction. As illustrated in Figure 1, even a small change in the weights can lead to significant change in the loss (or error) surface.

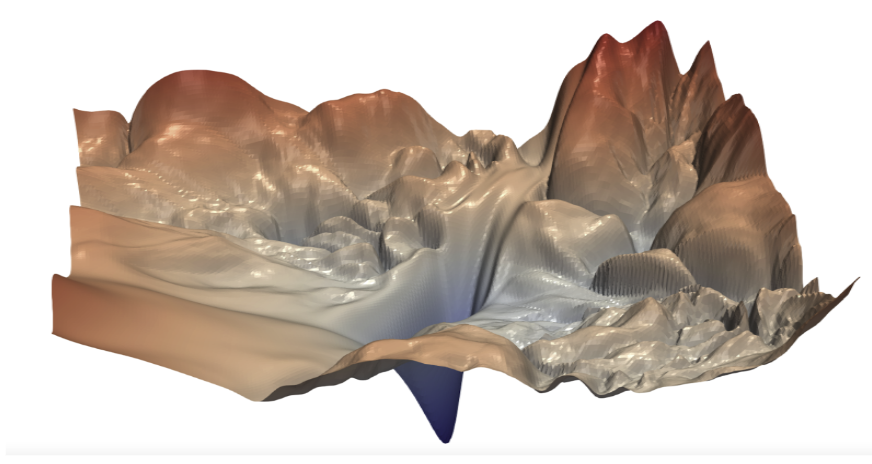Figure 1. The loss surface of ResNet-56 without skip connections by Hao Li et al¹

The quantization scheme used and the accuracy of the quantized model depend heavily on the network architecture and on the distribution of the weights and the activations. Figure 2 is an overview of  the impact of the quantization schemes on popular network architectures². Larger models like ResNet and Inception are relatively immune to quantization schemes than efficient models such as MobileNet. Simpler schemes, such as symmetric per tensor quantization, work well for large models but significantly degrade the accuracy of models designed for efficiency. It is critical to choose an architecture that is the best trade-off between computational performance and quantization accuracy.

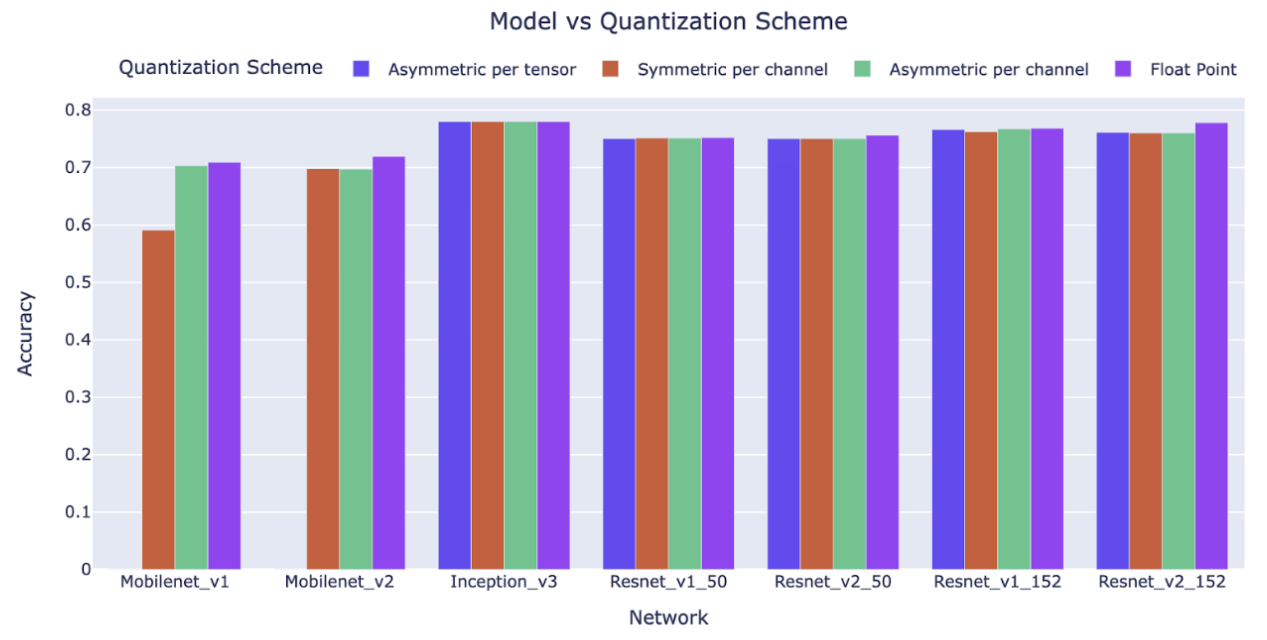Figure 2. Evaluation of  model accuracy for different quantization schemes

Quantization Analysis

Figure 3 shows various sources of error in a quantized implementation of a convolution operation. The bit precision used for different components ultimately depends on the model accuracy requirements. For example, the bias is quantized to 32-bit precision because networks are sensitive to bias errors which directly affect the output result. Moreover, the bias values don’t contribute much to the overall size of the network. Similarly the accumulators used for convolution results can use higher bit widths to avoid any potential overflow or clipping.

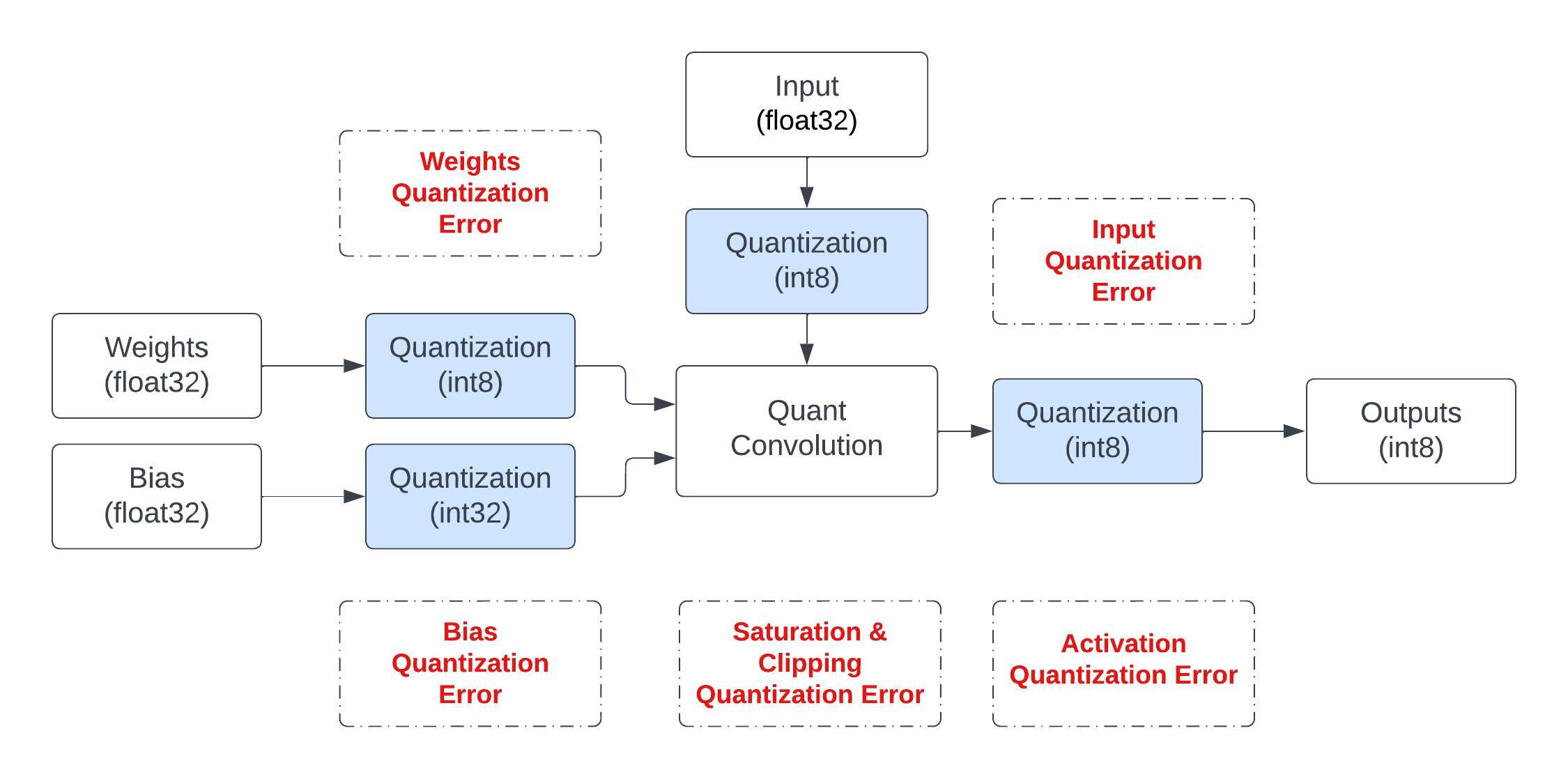Figure 3. Various sources of quantization error for a fixed-point convolution operation³

In the following section we discuss a few useful techniques to analyze these errors, which vary in scope from network level to single operation level.

Layerwise Error

When quantizing a model we should ensure that all layers have quantization support or have float-point fall back if needed. In many cases, large quantization errors can be attributed to only a few problematic layers. Popular frameworks such as TFlite and Pytorch provide tools for layerwise quantization error analysis that enables users to identify problematic layers and fix them. Figure 4 shows the dynamic range (left) and root mean square (RMS) error (right) per layer in a model. As an example,  layers with high RMS error, say > 0.5, could be run in floating point precision to recover accuracy loss.

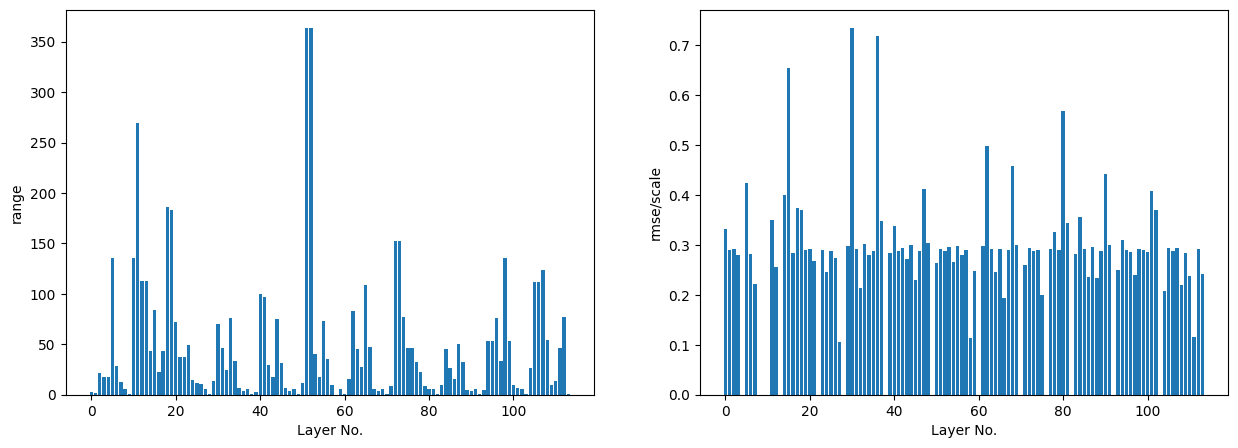Figure 4. Layerwise analysis of range and RMS error for quantized activations using TFlite

Min/Max Tuning Techniques

Quantization parameters are determined based on the min/max ranges of the distribution as discussed in Article I. Min/max tuning is used to eliminate outliers in weights and activations that could cause the remaining weights and activations to be less precise. These ranges are determined  differently for weights and activations. Weights, being fixed for a trained model, are easy to quantize. However, activation distribution depends on the input statistics which may be gathered during training or via a calibration dataset post training.

Absolute min/max method

This method sets the quantization range based on the maximum/minimum absolute value in the input data.

Percentile method

This histogram-based method uses percentiles to select the quantization range. This percentile represents a portion of the distribution, typically 99%, which clips the highest 1% of the magnitude values. This approach efficiently removes outliers that could impact quantization accuracy.

Entropy method

In this method, min/max values are chosen to minimize the distribution entropy using KL divergence between the original floating-point values and their quantized counterparts. This method, default in TensorRT, is beneficial when not all tensor values are equally significant for quantization purposes.

MSE method

This method minimizes the mean squared difference between the original floating-point values and the quantized values.

The accuracy results in Table 1 show how different min/max tuning methods affect the quantized accuracy of a model^6,8.

Model	Float	Max	Percentile	Entropy	MSE
ResNet50	0.846	0.833	0.838	0.840	0.839
EfficietNetB0	0.831	0.831	0.832	0.832	0.832
MobileNetV3Small	0.816	0.531	0.582	0.744	0.577

Table 1. Accuracy results for different min/max tuning methods on CIFAR100 dataset

Mixed Precision

Mixed precision refers to using multiple precisions in a single model. Using larger bit-width than 8-bit, e.g., 16-bit or FP16, is an effective way to mitigate quantization error and hence improve model accuracy. Various studies show how different bit widths for quantizing weights and activations affect the accuracy of a network⁵. Table 2 shows the accuracy of three different architectures where mixed precision is used to recover the accuracy loss incurred when the model was 8-bit quantized⁶. Note that compute efficient models like EfficientNet and MobileNet benefit substantially from mixed precision quantization.

Model	FP32 Accuracy	FP16 Quantization	INT8 Quantization	INT16 Activation	Mixed (FP32 + INT8) precision
ResNet50	0.8026	0.8028	0.8022	0.8021	0.8048
EfficietNetB2	0.8599	0.8593	0.8083	0.8578	0.8597
MobileNetV3Small	0.8365	0.8368	0.4526	0.7979	0.8347

Table 2. Evaluation of mixed precision accuracy on CIFAR10 dataset

3.4  Weight Equalization

Large differences in weight values for different output channels can cause larger quantization errors. Asymmetric/Symmetric per channel quantization helps in dealing with this variance in the weight distribution. However, many modern compute efficient networks like MobileNet/EfficientNet need per tensor quantization³, which uses the same quantization parameters across all channels in the tensor. This is a problem when there is a high variation in weights across channels. Weight equalization⁴ is an effective way to reduce the variance of weight distribution across channels. This approach adjusts the weights for each output channel to ensure their ranges are more evenly scaled. It broadens the range of values that are too low and narrows down the range of values that are too high.  This strategy relies on utilizing scale equivariance across layers with point-wise linear activation functions, which modifies the weight distribution without impacting the model’s output. Figures 5 and 6 show this process.

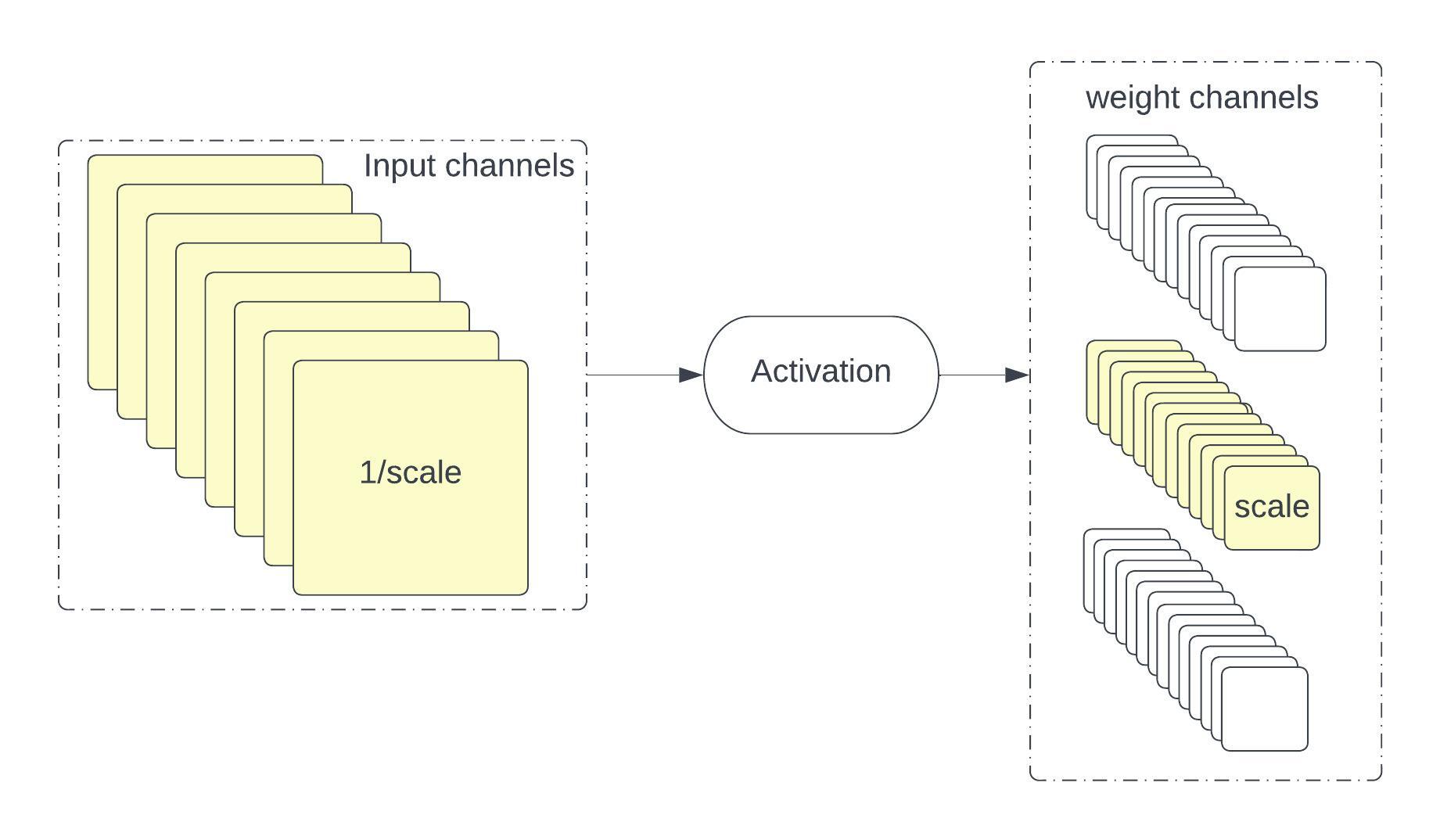Figure 5. Illustration of scaling channels for cross-layer weight equalization

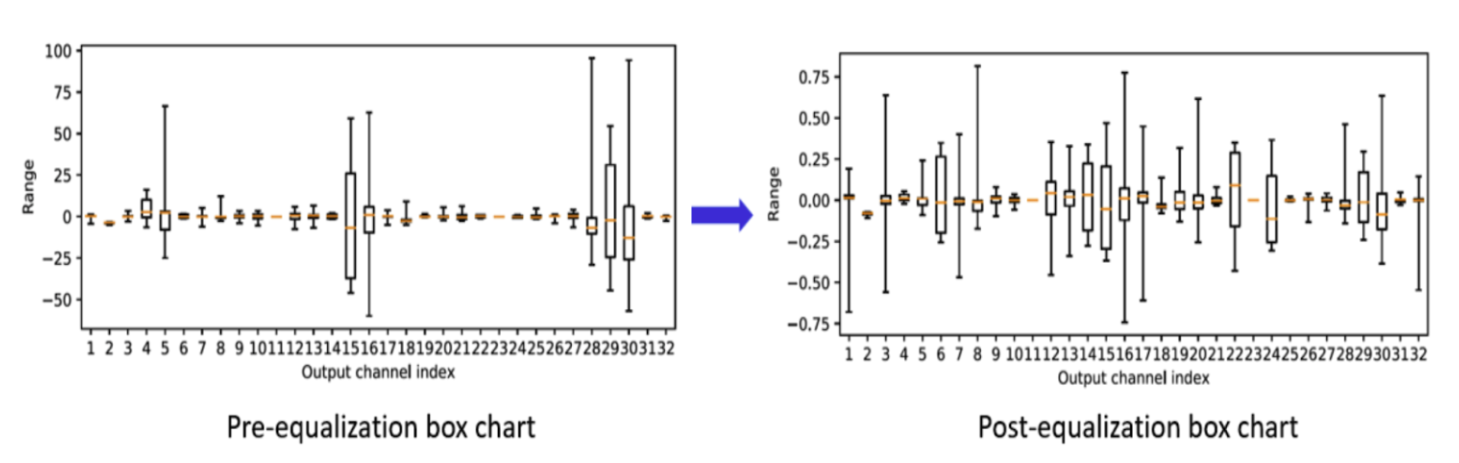Figure 6. Visualisation showing pre/post-equalization of weights⁷

Visualization 

Visualization of the weights and activations values allows us to observe their distribution. This is a powerful tool that gives the user the ability to estimate the effects of quantization on network accuracy and come up with approaches to minimize them.

Figures 7(a) and 7(b) show the quantized values for weights and activations clipped to a given min/max range. Distributions with longer tails tend to have higher error due to min/max limiting,  while skewed distributions have higher error due to the inefficient use of the available quantized range.

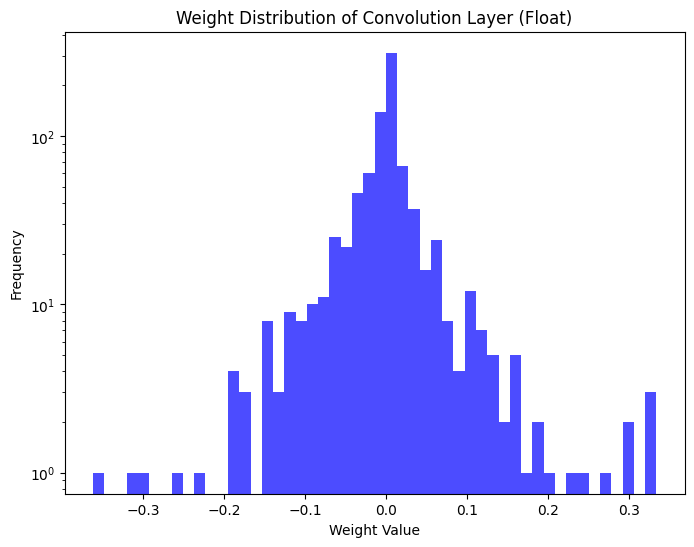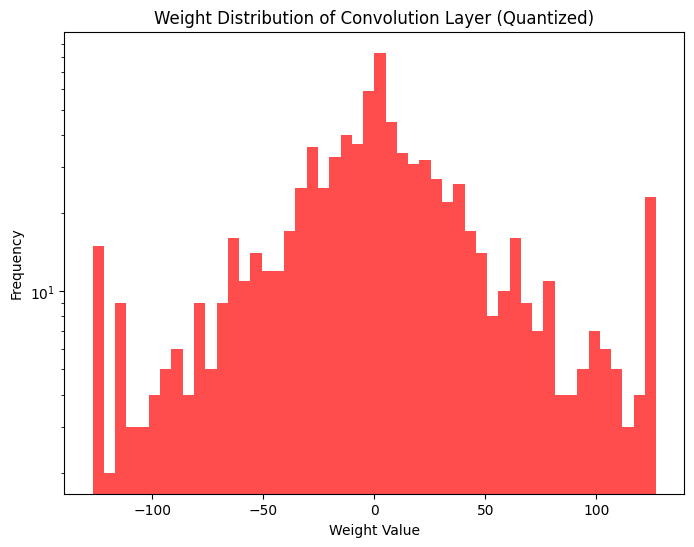Figure 7a. Weight distribution of MobileNetV2 first convolution layer: float and quantized

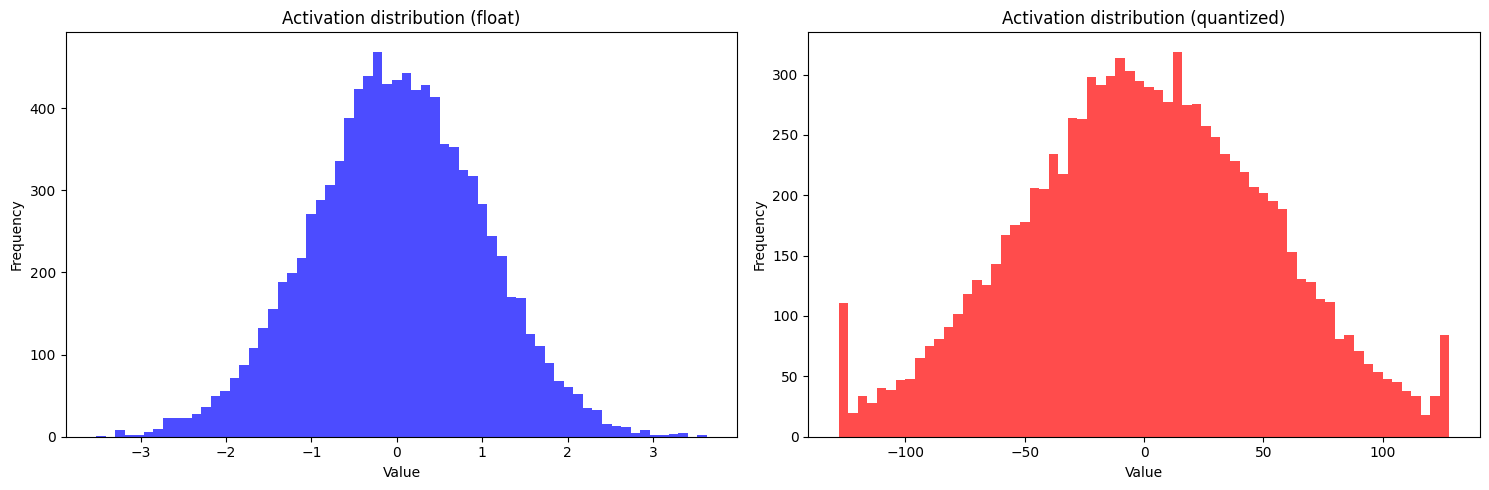Figure 7(b). Activation distribution of MobileNetV2 first convolution layer: float and quantized

Best Practices

In this section, we will summarize best practices for efficiently quantizing a model for implementation on an embedded device.

Model Selection

Efficiency of quantization is a function of the model size and its architecture. Large models are more tolerant of quantization error. NAS for efficient architecture for quantization and hardware aware model optimization, provides the best performance on device.

Model Quantization

Post Training Quantization (PTQ) is favoured for its efficiency, needing only a small representative dataset. Quantization-Aware Training (QAT) is resource-intensive but effective in regaining lost accuracy. It employs fake quantization during training to simulate quantization errors and refine the model.

Calibration Dataset

PTQ requires fine-tuning with a representative calibration dataset matching inference inputs. Statistical data from around 100-1000 samples can adequately model the data distribution to prevent bias in the quantized network.

Quantization Aware Training

Fine-tuning a pre-trained model for quantization accuracy can restore it to within < 1% of the floating-point model’s accuracy. While computationally expensive, this process is valuable for applications prioritizing accuracy.

Quantization Tools

Availability of quantization related tools dictate the quantization schemes and analysis that can be done during model quantization. TFlite and Pytorch quantization tools allow for different quantization schemes, analysis tools, and QAT, for improving a quantized model’s accuracy.

Quantization Scheme

Symmetric-per-channel quantization is recommended for model weights with a fixed distribution. For activations, asymmetric per-tensor quantization is advisable due to its flexibility in handling diverse activation values.

Quantization Evaluation

The network’s performance relies on various factors, including architecture and quantization. Before delving into quantization error analysis and debugging, it is recommended to assess the quantized model accuracy across different schemes.

Quantization Analysis

There are various sources of quantization error that affect the quantized accuracy of the network. In case of catastrophic failures, it is helpful to identify potentially problematic layers through layer-wise analysis. Once identified, the lost accuracy could potentially be recovered through techniques like mixed precision, min/max tuning, and weight equalization.

Conclusion

In this series of articles, we delved into the basics of quantization, explored various methods for model quantization, and examined techniques for analyzing quantization errors. We also discussed the tools and support available for these quantization schemes and analysis methods. As we conclude this exploration, we’ve outlined best practices for quantizing CNNs to achieve optimal computational performance and maintain quantized accuracy.

Dwith Chenna
Senior Computer Vision Engineer, Magic Leap

References

1. Hao Li, Zheng Xu, Gavin Taylor, Christoph Studer, and Tom Goldstein. Visualizing the loss landscape of neural nets. In Advances in Neural Information Processing Systems, pages 6389–6399, 2018.
2. Raghuraman Krishnamoorthi. Quantizing deep convolutional networks for efficient inference: A whitepaper. arXiv preprint arXiv:1806.08342, 2018.
3. Dwith Chenna, Quantization of Convolutional Neural Networks: A Practical Approach, International Journal of Science & Engineering Development Research, Vol.8, Issue 12, page no.181 – 192, December-2023, Available :http://www.ijrti.org/papers/IJRTI2312025.pdf
4. Nagel, M., van Baalen, M., Blankevoort, T., and Welling, M. (2019). Data-free quantization through weight equalization and bias correction.
5. Dwith Chenna, Edge AI: Quantization as The Key to on-Device Smartness, International Journal of Artificial Intelligence & Applications (IJAIAP), 1(1), 2023, pp. 58-69.
6. https://github.com/cyndwith/Quantizing-Convolutional-Neural-Networks-for-Practical-Deployment
7. S. Siddegowda, M. Fournarakis, M. Nagel, T. Blankevoort, C. Patel, and A. Khobare. Neural network quantization with ai model efficiency toolkit (aimet). arXiv preprint arXiv:2201.08442, 2022.
8. https://docs.deci.ai/super-gradients/latest/documentation/source/welcome.html